DIRECTED NUMBERS

Directed numbers

  • Directed numbers are numbers that have a sign (positive or negative) associated with them. 
  • They help us represent quantities that can have opposing directions or values.
  •  Positive-directed numbers indicate a gain or movement in the positive direction, while negative-directed numbers represent a loss or movement in the negative direction.

Directed numbers can be positive or negative numbers. These numbers are characterized by size (2 and 4.8) and direction (– or +).

Positive numbers: +3, +1.5, +0.2, +2, …

Negative numbers: – 3, – 1.5, -0.2, -21, …

Remember:

+3 is read as “positive three.”

+1.5 is read as “positive one point five.”

-3 is read as “negative three.”

-0.2 is read as “negative zero point two.”

Operations Involving Directed Numbers

The following are the rules for dealing with addition, subtraction, multiplication, and division of directed numbers.

Addition

There are two rules:

1. SAK (Same sign – Add – Keep the sign)

Examples:

(-2) + (-3) = -5                  

(-3) + (-4) + (-1) = -8     

2. DSB (Different sign – Subtract – copy the sign of the bigger number)

Examples: 

(-4) + (7) = 3

    (2) + (-8) = -6

Subtraction

Change the sign of the subtrahend to its opposite, then change the operation to addition. 

Examples: 

(-3) – (5) = (-3) + (-5) = -8

Notice that the subtrahend, 5, was changed into -5, and then the operation was changed to addition.

Multiplication and Division 

To multiply or divide integers, perform the operation as in whole numbers and then follow the rule for signs. 

Same Signs: the answer is positive.

Different Signs: the answer is negative. 

Examples:

       (-2) (-3) = 6                          (24) ÷ (-3) = – 8

      (8) (-2) = -16                       (-54) ÷ (-9) = 6

Examples with Solutions

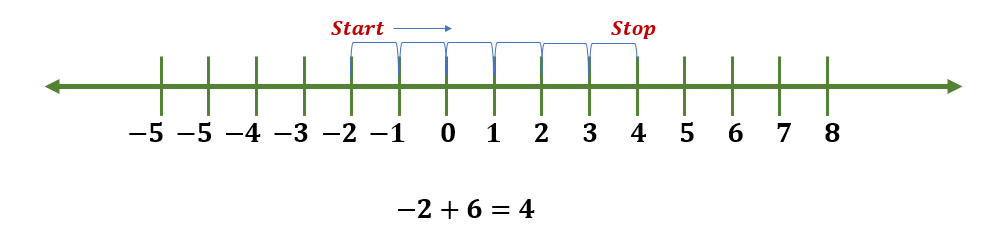
Example 1

Use the number line to solve -2+6.

Solution

Example 2

Find the sum of -7 and 5.

Solution

Since the numbers have different signs, we find the difference between their magnitudes: 7 – 5 = 2. The result will have the sign of the number with the larger magnitude, which is -7. So, the sum is -2.

Example 3

Subtract -4 from 3.

Subtracting -4 is the same as adding its opposite. The opposite of -4 is 4. So, we need to find the sum of 3 and 4, which is 7.

Example 4

Find the absolute value of -9.

Solution

The absolute value of -9 is the distance from -9 to 0 on the number line, which is 9.

Example 5

Add -3 and -6.

Solution

We add their magnitudes: 3 + 6= 9 since both numbers have the same sign

. The sum will have the same sign as the original numbers, which is negative. So, the sum is -9.

Example 6

Perform the indicated operations: (2 + -3) x (-8).

Solution

Let us simplify the parentheses first, then multiply.

(2 + -3) x (-8) =                                

(2 + -3) = -1

(-1) x (-8) = 8

%%%%%%%%ALL THE BEST%%%%%%%%


Comments

  1. Pauldasantus20 August 2024 at 23:38

    This is great bro keep it up with the good job

    ReplyDelete
  2. Ndinnah21 August 2024 at 00:14

    Who ever missed this lesson in class can come here for further explanation,this is incredible work

    ReplyDelete

Post a Comment

Popular posts from this blog

INDICES

Image
Please click the following links below, it can help you more on how to deal with INDICES topic in Mathematics.  1st link it's an audio while 2nd link it's a video. Please click it, all of them they are explaining the same thing, but have a different understandable.  https://drive.google.com/file/d/1ZUu2yl5VYPmvIc6R46_hvfMoDwvhs8N6/view?usp=drivesdk https://drive.google.com/file/d/1QGN9PyGlxIbsTF334SHdWMa8309qphPp/view?usp=drivesdk Thank you 😊 for listening👂 and Watching 👀, please don't forget to follow, comment and share.
Read more

NUMBERS AND OPPERATIONS

Image
  Real numbers system These are the set of all counting numbers such as 1,2,3,4,5,6,7,8,9, ...... Real numbers are numbers that include both rational and irrational numbers. Rational numbers such as integers (-3, 0, 2), fractions (1/2, 3.5) and irrational such as √3 ,π(22/7), are all real numbers NB: 1.   Under Integers there's negative numbers (-1; -2...) and whole numbers (0;1;2;3....)                   2. Under Whole numbers there's Natural numbers (1,2,3). Remember that 0 is not a natural                             number.                   3. Under Natural numbers there's Prime numbers (2;3;5;7......) and Composite number                                     (4;6;8;9....). May you please study this picture it...
Read more

Sequences

Image
  Sequences A sequence is a list of numbers in a specified order. The different numbers occurring in a sequence are called the terms of the sequence. Let the terms of a sequence be a 1 , a 2 , a 3 , …, a n , …, etc. The subscripts indicate the position of the term. That means, First term = a 1 Second term = a 2 Third term = a 3 …. The nth term is the number at the nth position of the sequence and is denoted by a n . This term is also called the general term of the sequence. Sequences Rules All the terms of a sequence possess a certain rule upon which the successive terms are defined. In the above examples, the sequence 3, 9, 27, 81…,59049 indicates the rule as the powers of 3. Here, each succeeding number will be obtained by multiplying the previous term with 3. Similarly, the set of even numbers also contains a rule that each successive term is obtained by adding 2 to the previous term. Based on these rules, we can define the general term of the sequences. This can be done as give...
Read more