Functions

 Functions

A function is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output. Let A & B be any two non-empty sets; mapping from A to B will be a function only when every element in set A has one end and only one image in set B.

Example:

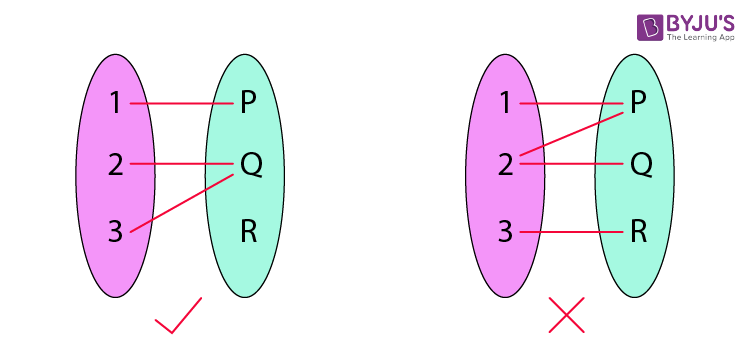
Another definition of functions is that it is a relation “f” in which each element of set “A” is mapped with only one element belonging to set “B”. Also, in a function, there can’t be two pairs with the same first element.

Condition for a Function

Set A and Set B should be non-empty.

In a function, a particular input is given to get a particular output. So, a function f: A->B denotes that f is a function from A to B, where A is a domain, and B is a co-domain.

• For an element, a, which belongs to A, a ∈ A, a unique element b, b ∈ B is there such that (a,b) ∈ f.

The unique element b to which f relates a is denoted by f(a) and is called f of a, or the value of f at a, or the image of a under f.

• The range of f (image of a under f)
• It is the set of all values of f(x) taken together.
• Range of f = { y ∈ Y | y = f (x), for some x in X}

A real-valued function has either P or any one of its subsets as its range. Further, if its domain is also either P or a subset of P, it is called a real function.

Vertical Line Test:

A vertical line test is used to determine whether a curve is a function or not. If any curve cuts a vertical line at more than one point, then the curve is not a function.

Functions are generally represented as f(x).

Let, f(x) = x3.

It is said as f of x is equal to x cube.

Functions can also be represented by g (), t(),… etc.

Question: Find the output of the function g(t) = 6t2 + 5 at

(i) t = 0

(ii) t = 2

Solution:

The given function is g(t) = 6t2 + 5

(i) At t = 0, g(0) = 6(0)2 + 5 = 5

(ii) At t = 2, g(2) = 6(2)2 + 5 = 29